主格模型
主格模型
主格和附属格: 单元格进行扩展的过程中,缺省情况下,相对于其右(下)边的单元格而言,扩展格是主动复制的,被称为其它格(其右/下的格)的主格,而其右(下)的单元格是被动跟随复制的,被称为扩展格的附属格或子格。主格和附属格是相对的概念,即某格是另一格的主格或附属格,不存在单独的主格和附属格。
从主格的定义中看,显然只有扩展格才能是其它格的主格!
要注意的是,在缺省情况下,扩展格左(上)的格并不是其附属格,只有右(下)的格才是其附属格。 特别地,某个单元格的主格属性可以人为被改变。
左主格和上主格: 单元格进行纵向扩展时,我们又称其为其它格(其右/下的格)的左主格,而横向扩展时则称为上主格。一个单元格可以既有左主格又有上主格。 特别地,某个单元格的左主格或者上主格属性可以人为的被改变,即可以人为的把某个纵向扩展格右边的单元格设为他的左主格,或者把某个横向扩展格下方的单元格设为他的上主格。
多层扩展: 多个单元格同时进行扩展时,一个扩展格可以既是某些格的主格又是另一个扩展格的附属格,这种情况下就形成多层扩展的情况。如果主格A1的附属格是B1,而B1还有附属格C1,那么B1称为A1的1级子格(或1级附属格),C1称为A1的2级子格(或2级附属格),同时A1称作B1的1级主格,A1称作C1的2级主格。如果C1再有附属格D1,那么A1是D1的3级主格,而D1是A1的3级子格。显然,B1是D1的2级主格,D1是B1的2级子格。
同一行(列)上有两个或更多的扩展格。左(上)边的扩展格将是右(下)边的扩展格的主格,右(下)边的扩展格是其左(上)边扩展格的附属格,同时又是其右(下)边单元格的主格。
图示:
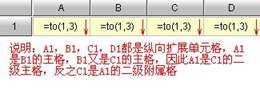
直接主格和直接附属格: 单元格进行多层扩展时,若主格A的附属格B不再有任何同方向的主格是该主格A的附属格,则称B为A在该方向上的直接附属格,也称为一级附属格;反之,A称为B的直接主格,也称为一级主格
扩展变化规则: 多层扩展时,扩展次序是从主到次的,即先扩展主格,然后扩展其附属格,再扩展其二级附属格,依此类推。
![[注意]](images/note.png) |
注意 |
|---|---|
| 单元格进行横向扩展时,会将其同列的上主格拉大,把其附属单元格复制,特别地,如果其某个上主格不在同列上,则该上主格不会被拉大;单元格进行纵向扩展时,会将其同行的左主格拉大,把其附属单元格复制,特别地,如果其某个左主格不在同行上,则该左主格不会被拉大。 |
一般地,主格能够主动进行扩展复制,称为主动扩展格;附属单元格被主单元格带动着复制,称为被动复制格。由于附属单元格同时又可能是别的单元格的主格,本身还可以进行主动扩展复制,因此主动扩展格和被动复制格是相对的。既不能主动扩展复制,也不能被动复制的单元格,我们称为不可复制格,或者叫固定格。
同一报表中可能同时有纵向扩展格和横向扩展格,如果它们的子格有重叠部分,则这些子格就即有左主格又有上主格,在扩展时会被即向下又向右复制,形成一片矩形单元格区域,从而做到交叉扩展。相应地,在这种机制下,多层交叉也不难实现。
在交叉扩展中,有的单元格有可能既被横向扩展向右复制,也被纵向扩展向下复制,可是,单元格的横向扩展与纵向扩展这两种扩展是相互独立的,既可以先进行横向扩展,也可以先进性纵向扩展,并不会影响扩展之后的结果。
例3.3.2-2:
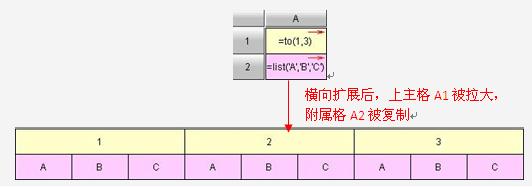
例3.3.2-3:
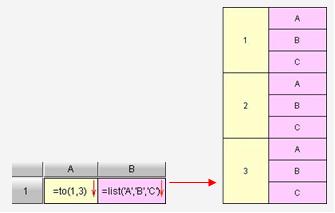
例3.3.2-4:
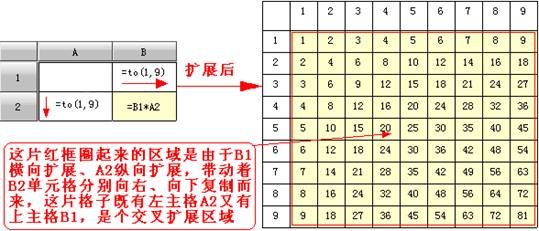
例3.3.2-5:
